Tal Alexander
Faculty of Physics
Weizmann Institute of Science
The phenomenon of black holes is one of the stranger consequences of General Relativity. The interest in these objects originates from two quite distinct perspectives.
From the perspective of basic theoretical physics, black holes are essentially elementary macroscopic objects, since their internal structure is causally disconnected from us. They can be fully characterized by three ``quantum'' numbers: mass, angular momentum and electrical charge. Black holes serve as ``gedanken-laboratories'' in attempts to reconcile quantum mechanics and General Relativity (e.g. Hawking radiation) and to explore the fundamentals of statistical mechanics and information theory (e.g. black hole entropy). Such thought experiments frequently require a microscopic black hole, where quantum effects are significant, or an isolated black hole in vacuum, where adiabatically slow thermodynamical processes can occur. Unfortunately, Nature does not appear to provide us with such black holes. All black holes that have been discovered so far are very massive, and are surrounded by, and interacting strongly with a hot radiating plasma (which also neutralizes any electric charge they may have). Thus, there is little hope of making an experimental connection between actual black holes and these fundamental questions of interest.
The questions of interest from the astrophysical perspective are very different from those of the fundamental physics perspective.
Two classes of black holes are known to exist. The first consists
of stellar black holes of roughly ![]() solar masses, which emerge
from the collapsing core of massive stars (
solar masses, which emerge
from the collapsing core of massive stars (![]() solar masses) that
have exhausted their nuclear fuel. The second consists of super-massive
black holes with masses in the range of
solar masses) that
have exhausted their nuclear fuel. The second consists of super-massive
black holes with masses in the range of ![]() to
to ![]() solar
masses, which are found at the centers of galaxies, one in each galaxy.
It is not exactly clear how super-massive black holes are formed.
A third class of yet undiscovered intermediate mass black holes is
also thought to exist. These may be the missing link between the stellar
black holes and the super-massive ones. This web essay will focus
on super-massive black holes, and specifically on the one in the center
of our home galaxy, the Milky Way.
solar
masses, which are found at the centers of galaxies, one in each galaxy.
It is not exactly clear how super-massive black holes are formed.
A third class of yet undiscovered intermediate mass black holes is
also thought to exist. These may be the missing link between the stellar
black holes and the super-massive ones. This web essay will focus
on super-massive black holes, and specifically on the one in the center
of our home galaxy, the Milky Way.
Black holes play a wide range of roles in current astrophysical research.
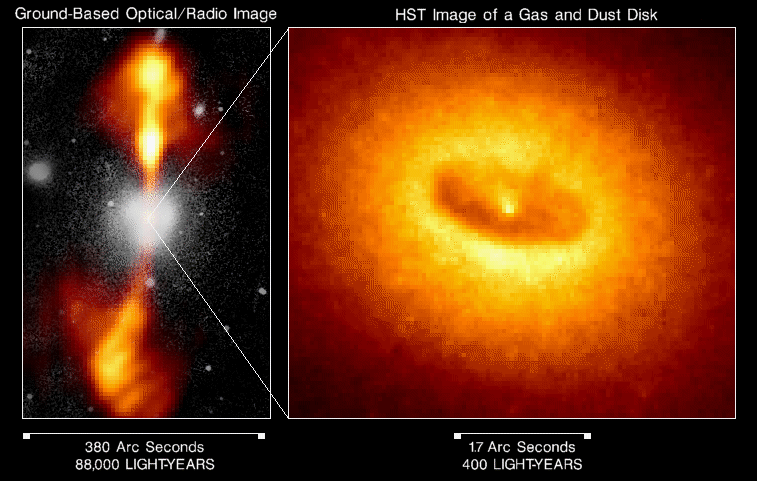
Left: A Hubble Space Telescope image of a disk of gas and dust in the inner 1000 light-years of active galaxy NGC4261. The gas is illuminated by an accreting massive black hole in the center. Right: The accretion also powers strong radio jets that extend well into intergalactic space. (Credits: National Radio Astronomy Observatory, California Institute of Technology, Walter Jaffe/Leiden Observatory, Holland Ford/JHU/STScI, and NASA. See Hubble Space Telescope press release. |

Composite infrared image of the Milky Way and its center. Large scale: COBE/DIRBE satellite image (1.25, 2.2 and 3.5 micron). Small scale: a 2MASS survey (1.25 and 2.17 micron) image combined with one from the MSX/SPIRIT satellite (6-11 micron). |
Like all galaxies, the Milky Way harbors a massive black hole. It
is the lowest mass black hole discovered to date, with ''only''
![]() solar mass (Eisenhauer et al. 2005; Ghez et al. 2005),
in keeping with the atypically small bulge of the Milky Way. Like
central black holes in many other galaxies, the Galactic black hole
is very dim. What makes this black hole unique is its proximity. It
is about 100 times closer than the black hole in the nearest large
galaxy, Andromeda, and about 2000 times closer than those in the galaxies
of the nearest cluster of galaxies, the Virgo cluster. For this reason
it is possible to observe the environment of the Galactic black hole
at a level of detail that will not be possible for any other galaxy
in the foreseeable future.
solar mass (Eisenhauer et al. 2005; Ghez et al. 2005),
in keeping with the atypically small bulge of the Milky Way. Like
central black holes in many other galaxies, the Galactic black hole
is very dim. What makes this black hole unique is its proximity. It
is about 100 times closer than the black hole in the nearest large
galaxy, Andromeda, and about 2000 times closer than those in the galaxies
of the nearest cluster of galaxies, the Virgo cluster. For this reason
it is possible to observe the environment of the Galactic black hole
at a level of detail that will not be possible for any other galaxy
in the foreseeable future.
The first hint of its existence was provided by the discovery, 30
years ago, of the unusual radio source Sagittarius A![]() (SgrA
(SgrA![]() )
at the dynamical center of the Galaxy (Balick and Brown 1974). It took
almost three decades to obtain decisive observational evidence that
SgrA
)
at the dynamical center of the Galaxy (Balick and Brown 1974). It took
almost three decades to obtain decisive observational evidence that
SgrA![]() is indeed a massive black hole. There were several
reasons for the long wait. The faint radio luminosity of SgrA
is indeed a massive black hole. There were several
reasons for the long wait. The faint radio luminosity of SgrA![]() could be easily explained in terms of other, less exotic alternatives.
Accreting massive black holes typically emit most of their luminosity
in the UV to soft X-ray range of the spectrum (the more massive the
black hole, the less energetic the typical wavelength). However,
most of this spectral range is not accessible to observations, since
the line of sight to the Galactic center is completely opaque to optical
to UV light (Figure 2) due to the large amount of intervening
interstellar dust (smog-like micron-sized particles made of graphite
and silicates). To see anything, it is necessary to observe in either
longer or shorter wavelengths. It is only recently that the Galactic
black hole was observed in the IR (Genzel et al. 2003a) and X-ray (Baganoff et al. 2001)
bands. Unfortunately, even these impressive observational achievements
are insufficient determine the nature of SgrA
could be easily explained in terms of other, less exotic alternatives.
Accreting massive black holes typically emit most of their luminosity
in the UV to soft X-ray range of the spectrum (the more massive the
black hole, the less energetic the typical wavelength). However,
most of this spectral range is not accessible to observations, since
the line of sight to the Galactic center is completely opaque to optical
to UV light (Figure 2) due to the large amount of intervening
interstellar dust (smog-like micron-sized particles made of graphite
and silicates). To see anything, it is necessary to observe in either
longer or shorter wavelengths. It is only recently that the Galactic
black hole was observed in the IR (Genzel et al. 2003a) and X-ray (Baganoff et al. 2001)
bands. Unfortunately, even these impressive observational achievements
are insufficient determine the nature of SgrA![]() --the physics
of accretion are still not understood well enough for the detection
of this emission to be considered strong evidence of the existence
of a black hole.
--the physics
of accretion are still not understood well enough for the detection
of this emission to be considered strong evidence of the existence
of a black hole.

Adaptive optics-assisted infrared images of the the central light year taken by the Very Large Telescope (Genzel et al., 2003a). The false colors correspond to temperature. Blue stars are hot and short-lived (therefore must be young). Red stars are old, less massive giant stars at the last stages of their lives. It should be emphasized that what seems to be the size of the stars is just an artifact due to light ``leaking'' around bright sources. At a distance of about 24000 light year all the stars are actually point-like sources well below the telescope's angular resolution. |
Most of the light emitted by the stars that orbit the black hole is also obscured by the inter-stellar dust. However, stars can be observed in the infrared, albeit with more difficulty (Figure 3). Recent technological advances in infrared astronomy enabled deep and precise observations of these stars as they orbit the black hole (Eisenhauer et al. 2005; Ghez et al. 2005). It was these observations that finally delivered the most convincing evidence for the existence of the massive black hole. This is because the stars are clean, direct probes of the gravitational potential, whereas gas can be affected by other forces, such as radiation pressure, thermal pressure and magnetic fields.

Stellar orbits around the massive black hole in the Galactic center, observed in the infrared (2.2 micron) with the Very large Telescope (Schödel et al. 2002; Eisenhauer et al. 2005). The actual measurements (points with error bars) are shown only for the star named ``S2''. S2 has the shortest orbital period (15.2 years) of the stars detected to date. Its distance of of closest approach to the black hole is only 17 light-hours, at which point it is traveling at almost 2% of the speed of light. For more information see MPE's Galactic Center web page. |
Figure 4 shows the reconstructed orbits of several of the
stars near SgrA![]() that were monitored over about a decade.
The stars appear to be in orbit around an empty spot in space. The
one star with the shortest period, S2, (15.2 yr) singly provided enough
information to resolve several key question about the mysterious dark
mass in the center of the Galaxy (Figure 5).
that were monitored over about a decade.
The stars appear to be in orbit around an empty spot in space. The
one star with the shortest period, S2, (15.2 yr) singly provided enough
information to resolve several key question about the mysterious dark
mass in the center of the Galaxy (Figure 5).
Using stellar orbits to answer fundamental questions about the dark mass in the center of the Galaxy. Top: The perfect (to within measurement errors) Keplerian elliptical orbit implies that the central mass is fully enclosed inside the point of closest approach, leaving few viable options other than a black hole to explain the central mass. Middle: the acceleration vectors from several orbits should all point to the center of acceleration, thereby identifying the position of the dark mass (this subsequently enabled a targeted search for the infrared emission from the accretion on the massive black hole, see Figure 6). Bottom: By combining measurements of line-of-sight velocity (in km/s) and angular velocity in (rad/yr) with the orbital solution, it is possible to measure the distance between the solar system and the black hole, that is, the distance to the Galactic center. | ||||||||||||||||||||||||||||||
One of the prime motivations for exploring the Galactic black hole
is to observe General relativistic phenomena close to a super-massive
object. The accretion luminosity is emitted by gas at distances only
a few times larger than the event horizon (the strong-field limit).
Not long after the center of acceleration was pinpointed, the black
hole was finally revealed when it flared in the infrared (Figure 6).
Such flares are now known to be fairly frequent, occurring a few times
per day, and typically lasting about an hour. It is thought that the
flares are triggered by temporary peaks in the mass supply rate to
the black hole, perhaps due to the presence of a denser than average
clump of gas in the accretion flow. Two of these flares displayed
an almost periodic fluctuation in their luminosity while the flare
lasted (Figure 7). The quasi-period of about 17 minutes is almost
half as short as would be expected for gas orbiting at the last stable
circular orbit of a
![]() , non-spinning
black hole. The black hole's spin affects the structure of space-time
around it in a way that draws the last stable circular orbit closer
and shortens its period. Thus, if indeed the flares arise from
gas orbiting for a few periods close to the last stable orbit, and
if the quasi-periodicity indeed reflects the orbital period,
it is possible to translate the 17 minutes period to a lower limit
the spin of the black hole, which must be spinning at half of its
maximal possible value (Genzel et al. 2003a). This is not surprising;
since the black hole absorbs the angular momentum of the matter that
falls in it, it is expected to spin quite substantially. Thus, it
is possible that the temporal structure of the flares is probing how
spacetime is twisted by the spinning black hole.
, non-spinning
black hole. The black hole's spin affects the structure of space-time
around it in a way that draws the last stable circular orbit closer
and shortens its period. Thus, if indeed the flares arise from
gas orbiting for a few periods close to the last stable orbit, and
if the quasi-periodicity indeed reflects the orbital period,
it is possible to translate the 17 minutes period to a lower limit
the spin of the black hole, which must be spinning at half of its
maximal possible value (Genzel et al. 2003a). This is not surprising;
since the black hole absorbs the angular momentum of the matter that
falls in it, it is expected to spin quite substantially. Thus, it
is possible that the temporal structure of the flares is probing how
spacetime is twisted by the spinning black hole.
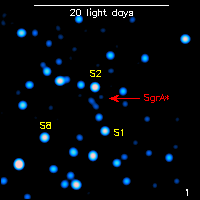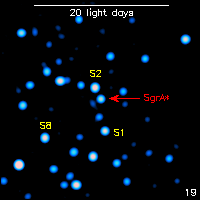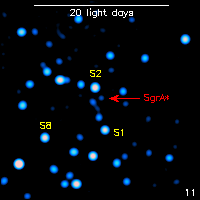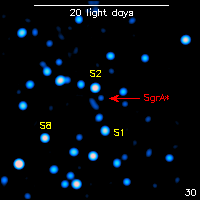
First observed infrared (2.15 microns) flare from the Galactic black hole, as detected by the Very Large Telescope. The animation is looped: one cycle corresponds to half an hour (Genzel et al. 2003a).For more information see MPE's Galactic Center web page. |

A 17 minute quasi-period in the flux during an accretion flare, possibly originating in a hot clump of gas that orbits right at the last stable orbit for a few times before finally falling into the black hole. The period at the last stable orbit of a non-rotating black hole with the mass of the Galactic black hole is predicted by theory to be 27 minutes. The shorter 17 minutes period is explained by the fact that spacetime warps differently when the black spins, resulting in a smaller last stable orbit and a shorter orbital period. (Genzel et al. 2003a) |
Typical stars cannot approach the Galactic black hole as close as
the emitting gas without being destroyed by the tidal field of the
black hole. Thus, stars can mostly probe the weak-field limit of General
relativity. Though less spectacular than the strong-field limit, stars
orbiting a million solar mass class object at up to a few percents
of the speed of light nevertheless probe a virtually unexplored regime
of relativistic celestial mechanics. One effect that will be hopefully
detected with continued monitoring is the slow-down of time near the
black hole (gravitational redshift), as expressed by the Doppler shift
of the stellar spectra. This effect is substantially larger at the
orbits' point of closest approach than it is on the surface of a white
dwarf. Another effect that may be eventually detected is the advancing
rosette-like orbits that are predicted by General Relativity (Figure 7)
as a consequence of the deviation from the Newtonian ![]() gravitational
force law.
gravitational
force law.

A schematic comparison of a classical Newtonian orbit around a point central mass (red) and a General Relativistic one (blue). In Newtonian physics the gravitational force falls exactly as the distance squared, and the orbital ellipse closes on itself. Close enough to the central black hole General Relativistic effects deviating from Newton's law of gravitation cause the point of closest approach to advance, leading to a rosette-shaped orbit (blue). |

Gravito-hydrodynamic simulations of fast stellar collisions in the dense stellar cusp near a massive black hole. Left: two equal mass stars (orange) in a grazing collision are momentarily deformed and evaporate a few percents of their mass (yellow clouds). Right: A neutron star (blue) in a penetrating collision with a normal star. |
Dynamical studies of the way stars respond to the growth and presence of a massive black hole in a galactic center all predict that the stellar density will grow toward the center and settle into a (formally) diverging, high density ``stellar cusp''. The observed stellar density near the black hole is about a billion times higher than near the Sun, and the stars move up to a 100 times faster relative to each other than they do elsewhere in the Galaxy (Alexander 1999; Genzel et al. 2003b). Such extreme and unique conditions effectively make the inner stellar cusp into a ``stellar collider'', where stellar properties can be probed when stars closely interact with each other or with the black hole. Many theoretical ideas involving stellar dynamics and stellar physics have been proposed to explain various aspects of the unusual stellar population that is observed near the Galactic black hole. The picture is still far from clear. We conclude this article by briefly mentioning just three of the many possible processes.

A gravito-hydrodynamic simulation of an extreme tidal interaction between a star and a massive black hole, that may lead to a nuclear run-away and a supernova explosion. Top left: a view of the stellar trajectory (orange) around the black hole (red dot) from above the orbital plane. Top right: An edge-on view of the orbit. Note how the star (black blob) is squeezed into a two-dimensional pancake as it passes through the point of closest approach. Bottom: a plot of the changes in the central density as function of time. The higher the central density, the faster the nuclear reaction rates. |

A schematic depiction of a celestial billiards ball game. The orbit of a hot young star (blue dot following dashed trajectory) approaching close to the black hole (big central black dot) intersects with the tight orbit of a stellar mass black hole (small black dot following solid trajectory) of roughly the same mass. As a result of a 3-body exchange, the young star ``knocks'' the stellar black hole away (the interaction is gravitational--the two don't actually touch each other) and takes its place in a tight orbit very close to the massive black hole. |
The Galactic black hole provides a uniquely accessible laboratory for studying in detail a massive black hole in its interactions with its environment: how it feeds and grows by accreting gas and stars and how the extreme density, high velocity and strong tidal fields affect the stars near it. The gas and stars probe the nature of the central dark mass and probe post-Newtonian gravity in the weak- and strong-field limits. These issues are relevant for understanding the massive black hole phenomenon in general. The wealth of observed phenomena near the Galactic black hole provides the impetus to study the physics of gas and stellar processes in such an extreme environment. These studies prove to be very fruitful, yielding valuable insights even in cases where they do not fully succeed to explain the observations (Alexander 2005). Many questions remain--the most exciting science still lies ahead.