The z-transformed discrete correlation function (ZCDF)
Astronomical time series are often too sparse and unevenly sampled to be inverted for analysis in the frequency domain, and the analysis is carried out in the time domain by the Cross-Correlation function (CCF)  and Auto-Correlation function (ACF). There are two approaches for dealing with the gaps in the data: interpolation and discrete binning. Interpolation becomes unreliable when there is significant power on time scales smaller than the typical gap size. The discrete correlation function  (DCF) method (Edeleson & Krolik 1988) avoids interpolation by binning the time difference pairs and calculating the mean and variance of each bin. The drawback of this method is that the DCF suffers from the same problems as the closely related linear correlation coefficient r, which measures the correlation between independently drawn pairs (x,y). The sample distribution of r is known to be very skewed and far from normal. 

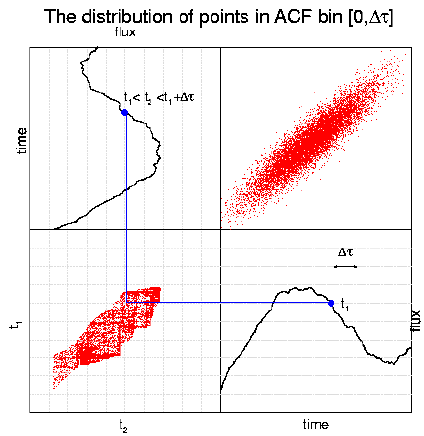
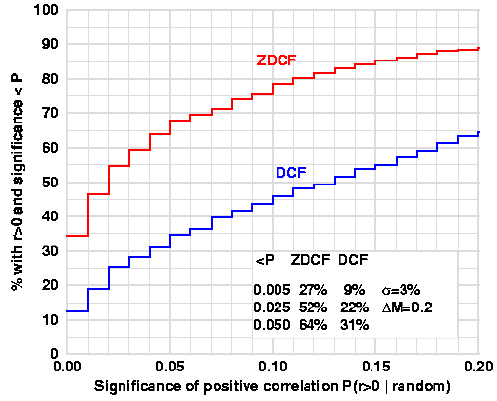
Fisher's z-transform of r  (Fisher 1920) is approximately normally distributed when (x,y) are drawn from a binormal distribution, and can therefore be used to estimate the confidence level of a measured correlation. Because the points in the light curve are not normally distributed and are auto-correlated, it is not immediately obvious that the z-transform is generally applicable for normalizing the DCF.  However, it is possible to show that under a wide range of conditions the ZDCF does provide significantly improved estimates of the CCF. Furthermore, a new algorithm for setting the bin sizes removes biases due to the number of data points in the light curve. This is important when comparing the CCF of different light curves.

More details about the ZDCF method and its advantages over the interpolation method and the untransformed DCF can be found in Alexander (1997).
A demonstration of the nature of the approximation that is involved in applying Fisher's z-transform to auto-correlated time series. The top left and bottom right panels show (the same) light-curve, whose ACF is estimated from randomly chosen pairs of points separated by no more than dt in time. The actual 2 dimensional distribution of the points (bottom left panel) is quite irregular, and reflects the structure of the  light-curve. This is compared to a binormal distribution (top right panel) with the same variances and covariance as the empirical distribution.

 
A comparison between the efficiency of the ZDCF and DCF in detecting a correlation between magnitude and variability time scale in a small sample of sparse simulated AGN light curves (30 light curves with 15 points each). The ZDCF has a 2 to 3 greater chance of detecting the correlation.
A FORTRAN 77 implementation of the  ZDCF algorithm can be downloaded from here. The instructions appear as comments at the head of the file. The ZDCF should be cited as T. Alexander, 1997, in Astronomical Time Series, Eds. D. Maoz, A. Sternberg, and E.M. Leibowitz, (Dordrecht: Kluwer), 163.

Questions, suggestions and bug reports are welcome (tal.alexander@weizmann.ac.il).  I would also appreciate receiving a short note about projects (and papers) where the ZDCF was put to good use.