Protocol for W1 theory

We thus propose the following protocol for a computational level which we will call W1 (Weizmann-1) theory:

• geometry optimization at the B3LYP/VTZ+1 level (B3LYP/VTZ if only first-row atoms are present). Alternatively, the B3PW91 exchange-correlation functional may be preferable for some systems like Cl₂ -- under normal circumstances, B3LYP/VTZ+1 and B3PW91/VTZ+1 should yield virtually identical geometries;
• zero-point energy obtained from B3LYP/VTZ+1 (or B3PW91/VTZ+1) harmonic frequencies scaled by 0.985;
• Carry out CCSD(T)/AVDZ+2d and CCSD(T)/AVTZ+2d1f single-point calculations;
• Carry out a CCSD/AVQZ+2d1f single-point calculation;
• the SCF component of TAE is extrapolated by A+B/C^l from SCF/AVDZ+2d, SCF/AVTZ+2d1f, and SCF/AVQZ+2d1f components of TAE (l=2, 3, and 4, respectively)
• set 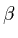$\beta$=3.22
• the CCSD valence correlation component is obtained from applying 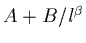$A+B/l^{\beta}$ to CCSD/AVTZ+2d1f and CCSD/AVQZ+2d1f valence correlation energies (l=3 and 4, respectively). In both this and the next step, it is immaterial whether the extrapolation is carried out on components to the total energy or to TAE;
• the (T) valence correlation component is obtained from applying 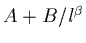$A+B/l^{\beta}$ results to CCSD(T)/AVDZ+2d and CCSD(T)/AVTZ+2d1f values for the (T) contribution.
• core correlation contributions are obtained at the CCSD(T)/MTsmall level;
• scalar relativistic and, where necessary, spin-orbit coupling effects are treated at the ACPF/MTsmall level. As in W2 theory, this latter step can be combined in a single job with the previous step.

W1 theory can be applied to fairly large systems (see below). CPU times are dominated by the inner-shell correlation contribution (particularly for second-row compounds), which is reflected in the relatively small time reduction compared to W2 theory -- e.g., from 1h12' to 24' for CO and from 13h42' to 8h48' for OCS. In addition -- contrary to W2 theory -- W1 theory exhibits a pronounced difference in performance between first-row and second-row compounds: for the species in Table VI, MAE is 0.26 kcal/mol for first-row, but 0.40 kcal/mol for second-row compounds. Since the CPU time gap between W1 and W2 theory is fairly narrow for second-row species, we conclude that for accurate work on second-row species -- unless precluded by disk space or memory limitations -- it may well be worth to `walk the extra mile' and carry out a W2 rather than a W1 calculation. For first-row systems, on the contrary, W1 may well seem the more attractive of the two.